First of all, I'm glad you're here. If we had a venn diagram of "software developers" and "people interested in FPL", it'd likely not be much more than us two. Rest assured, if you're only in the former camp I hope there will still be some things of interest. Also, disclaimer, I am by no means a FPL expert: I'm sitting rock bottom of my league with friends so think less Liverpool, more Southampton. Perhaps if it were possible to predict what would happen in a game of football (assuming I'm smart enough to even do so), it wouldn't be the most popular sport in the world.

The code for this post can be found in my Github repo here.

TL;DR

For those that just want FPL tips, here is (probably) the best FPL team, not that it'll get you very far:

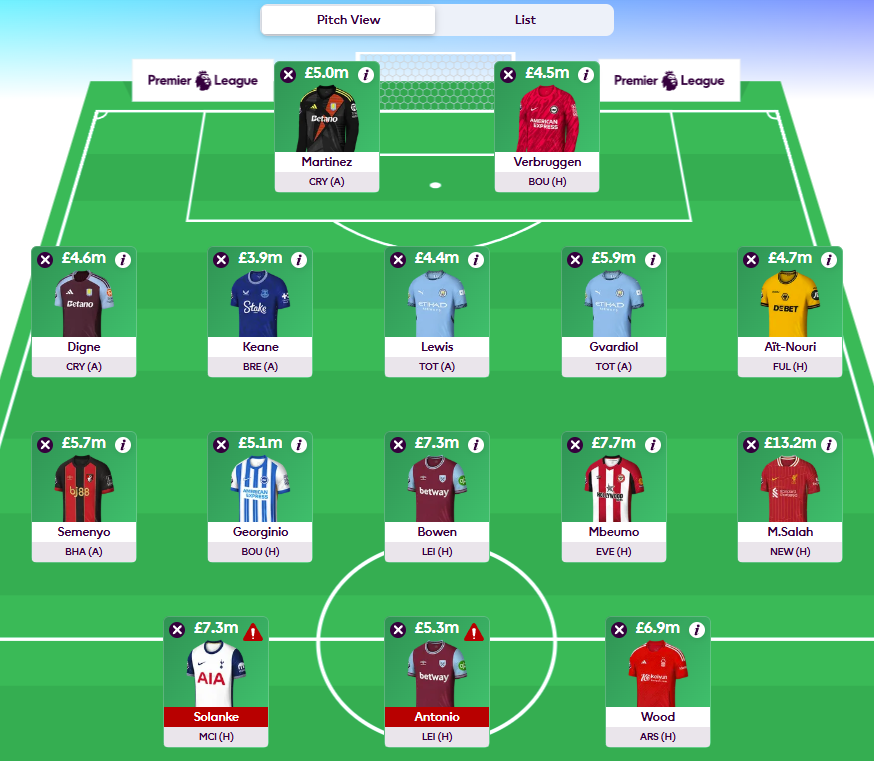
This team is picked based on how many points each player is predicted to score (which I'll go into later).

What is FPL?

FPL means Fantasy Premier League. It's a game where you pick a team of players, and your team scores points based on real-live events in premier league games. Here are the rules:

1. Pick 15 players: 2 goalkeepers (GK), 5 defenders (DEF), 5 midfielders (MID), 3 forwards (FWD).
2. You can't have more than 3 players from a specific team.
3. The cost of your team can't exceed the budget of 100M.

There are around 700 players for 20 different clubs, that's a lot of possible teams. To save this becoming a post on discrete maths, that a lot of possible teams. But what's the "best" team to pick? What criteria do we use to make this decision? This is what's known as a "combinatoral optimisation" problem, and that's where Google OR Tools comes in.

What is Google OR Tools?

Google OR Tools is an open source library that allows you to solve problems like this. You can use it in Java, C++, Python and, for our purposes, in C#. The documentation linked here is decent, so I wont go into too much detail as to how it all works. For our use case we're essentially going to ask OR Tools to solve many IntVars. That is, variables which must take an integer value based on the provided upper and lower bounds. We'll give our IntVars bounds of [0,1] so that if a player is picked that means its corresponding IntVar will have a value of 1. The complexity comes in telling the CpModel what decisions to make based on a player being picked.

I found it useful to create a child class of OR Tools' CpModel so I can easily keep track of variables that I want to add constraints for:

public class PickFplTeamCpModel : CpModel
{
    public List<FplPlayerSelectionVar> GkSelections = [];
    public List<FplPlayerSelectionVar> DefSelections = [];
    public List<FplPlayerSelectionVar> MidSelections = [];
    public List<FplPlayerSelectionVar> FwdSelections = [];    
    public Dictionary<string, List<IntVar>> TeamSelectionCounts = new();

    public List<FplPlayerSelectionVar> Selections => GkSelections
        .Concat(DefSelections)
        .Concat(MidSelections)
        .Concat(FwdSelections)
        .ToList();
}

FplPlayerSelectionVar is a record that contains the player's details, as well as their selection variable.

Now, let's add our constraints.

Rule #1: 2 GK, 5 DEF, 5 MID, 3 FWD

We need to make sure we have the right number of players in each position. We can do this by using the properties on our child class of CpModel:

// Sum up the selections for each position, and ensure it matches the number of players required per position.
model.Add(new SumArray(model.GkSelections) == 2);
model.Add(new SumArray(model.DefSelections) == 5);
model.Add(new SumArray(model.MidSelections) == 5);
model.Add(new SumArray(model.FwdSelections) == 3);

A SumArray is an OR Tools object. that sums an array of IntVars. Think of it as a "computed" field, dependent on other IntVars. By doing model.Add we adding a hard constraint to the model. This means that if a solution were to be found that picked only 4 defenders, the solution would be infeasible.

Rule #2: max 3 players per team

Our TeamSelectionCounts is a dictionary, keyed by team name. We can tell the model to not pick too many players from the same team as follows:

foreach(var (_, selectionsForTeam) in model.TeamSelectionCounts)
{
    // This sums up all the 0's and 1's for a team.
    var playersSelectedForTeam = new SumArray(selectionsForTeam);
    model.Add(playersSelectedForTeam <= 3);
}

Rule #3: squad cost

This one's a bit more involved as we're not simply summing up 1s and 0s, we're summing up player costs based on these values. If you've done any work with vectors before you might have come across dot product operations. We're going to use this to sum up the cost of all selected players. That is, the dot product of their selection vars and their costs. The FplPlayerSelectionVar type contains these pieces of information:

public record FplPlayerSelectionVar
{
    public IntVar Selected { get; init; }
    public int Cost { get; init; }
    public decimal PredictedPoints { get; init; } 
}

We'll get to PredictedPoints later. By keeping this information together, we can easily sum up the costs of selected players like so:

var allPlayerSelections = model.Selections.Select(p => p.Selected).ToList();
var allPlayerCosts = model.Selections.Select(p => p.Cost).ToList();
var squadCost = LinearExpr.ScalProd(allPlayerSelections, allPlayerCosts);
model.Add(squadCost <= 1000);

Note: we're using 1000 rather than 100 because player cost is represented in 100,000s e.g if a player cost 7.9M, their int Cost would be 79.

LinearExpr.ScalProd does the dot product as described earlier.

The objective

At this point, we have a feasible solution to the problem. I could go into the web app and click "Save" without any validation preventing me from doing so. If this were purely a constraint solving problem (e.g doing a Sudoku is a good example of this) where no two solutions are better than another we'd be done. However, we want the best team: I want to wipe the floor with my friends and be the envy of FPL merchants everywhere.

In order to say an FPL team is the best possible team, the model needs to be able to compare two solutions together, and say one solution is better than another. OR Tools gets all feasible solutions, labelling the one with the best score as the optimal solution. In order to change this into an optimisation problem, we need to give the model an objective.

This is where it gets quite squishy. If we knew for certain how many points a player would score in a given game, other than that being a very boring prospect, I'd be doing a lot better in my FPL leagues than I currently am.

So what do we go with?

Selection-y-est: we could pick the players most selected by other players. Using this hive-mind approach would mean we're more likely to pick the no-brainers, but the model wouldn't give us any hipster choices that would make other players go "how did I not think of that?!".

Point-y-est: we could pick the ones who've scored the most points so far. This would make a lot of sense, but would not select players who've recently transfered, or have been out injured for a while.

Form-y-est: FPL has a concept of "form". However it's a bit black-boxed and it's not very clear how this is calculated, and therefore how it corresponds to the amount of points a player might score.

How about some combination of the above? I landed on putting together a very ropey linear regression model built with ML.NET. I won't go into how this model was built, but essentially it would use past performance to predict points scored by a player for the upcoming gameweek. Inexplicably, this model was obsessed with Georginio Rutter; a very average player by FPL standards. Reassuringly, it consistently predicted that Mo Salah would score highly so I decided it was "good enough". If there were reliable, publicly available information about a player's expected points (XP), I would swap out my linear regression model without hesitation.

Here's how I told the model to pick me a team with the highest predicted points:

var allPlayerPredictedPoints = model.Selections.Select(p => (int)Math.Round(p.PredictedPoints * 100)).ToList();
var allPlayerSelections = model.Selections.Select(p => p.Selected).ToList();
var teamPredictedPoints = LinearExpr.ScalProd(model.Selections, allPlayerPredictedPoints);
model.Maximize(teamPredictedPoints);

The important bit here is model.Maximize, this means the model's solution will be the one with the highest calculated teamPredictedPoints.

In practice

Lets put all this together. Here are the top players in terms of predicted points for the upcoming gameweek (this is GW26 on 22nd Feb 2025):

Rank	Player	Team	Position	XP
1	Antoine Semenyo	BOU	MID	10.3
2	Bryan Mbeumo	BRE	MID	10.3
3	Mohamed Salah	LIV	MID	9.4
4	Georginio Rutter	BHA	MID	9.3
5	Jarrod Bowen	WHU	MID	9.2
6	Joško Gvardiol	MCI	DEF	8.5
7	Rayan Aït-Nouri	WOL	DEF	8.5
8	Cole Palmer	CHE	MID	8.4
9	Brennan Johnson	TOT	MID	8.3
10	Diogo Teixeira da Silva	LIV	MID	8.1

An immediate observation is that we won't be able to pick all the players in this list due to fact that we can't have more than five midfielders. Chris Wood is the first FWD that appears in at #12 with a XP of 8.0, with Erling Haaland in at #17 with 7.2 (I hope not - he's playing Liverpool this weekend). Let's compare that with the team my model picked:

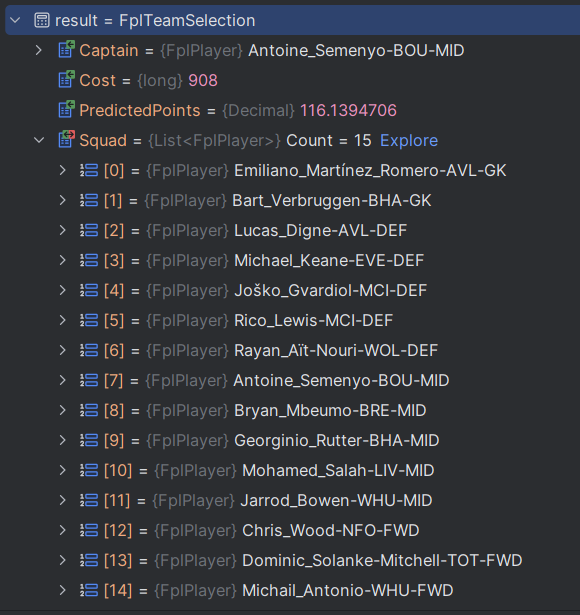
In table form:

Rank	Position-specific Rank	Player	Team	Position	XP
79	1	Emiliano Martínez Romero	AVL	GK	4.4
80	2	Bart Verbruggen	BHA	GK	4.3
20	3	Lucas Digne	AVL	DEF	7.0
28	5	Michael Keane	EVE	DEF	6.3
6	1	Joško Gvardiol	MCI	DEF	8.5
27	4	Rico Lewis	MCI	DEF	6.6
7	2	Rayan Aït-Nouri	WOL	DEF	8.5
1	1	Antoine Semenyo	BOU	MID	10.3
2	2	Bryan Mbeumo	BRE	MID	10.3
4	4	Georginio Rutter	BHA	MID	9.3
3	3	Mohamed Salah	LIV	MID	9.4
5	5	Jarrod Bowen	WHU	MID	9.2
12	1	Chris Wood	NFO	FWD	8.0
18	3	Dominic Solanke-Mitchell	TOT	FWD	7.2
25	8	Michail Antonio	WHU	FWD	7.0

Let's check our rules:

1. ✅ 2 GKs, 5 DEF, 5 MID, 3 FWD
2. ✅ Max 3 players per team
3. ✅ Total team cost: 90.8M

The predicted number of points this team scores is 116.1.

Narrator: they did not. They scored 70 points.

Now, I've been scoring around 55 points on average per gameweek, so this would be a big change in fortunes. I'll need to choose four players to go on the bench here, so I reckon I would be happy with a score of 90. As you can see, the model ended up picking the five best midfielders. It may look like it picked any old goalkeeper, however the two listed here are in fact the highest ranked, followed by Martin Dúbravka at #98.

Next steps

As mentioned a few times, it isn't just self-deprecation, this application is far from perfect. I'd love to be able to tell you how I've soared up the FPL rankings since I started doing this, but that's not the case. These are the changes I'd like to make to the model in future.

Prioritise starting XI

The FPL squad has a size of 15, but you only score points for the 11 players you pick for the starting lineup. Therefore, why should we waste budget on benchwarmers that don't give me any points?

Transfers

You get a free transfer every game week and these cumulate if you don't use them. Any further transfers cost you 4 points. You get a wildcard twice a season which gives you unlimited transfers, but day-to-day gameweeks need to support the scenario of "I have these players, and X free transfers. Tell me what transfers to do".

Better XP

As mentioned above, this solution is only as good as the XP data is. I need to either work on my linear regression model, or find some XP data that's less fixated on Georginio Rutter.

Think more long-term

At the moment, we predict the points based on the next game, but sometimes we have double-gameweeks i.e a player plays twice. It also might be that a specific player has a particularly good run of easier opponents coming up, so getting them in the team now might make sense, even if they wouldn't do as well as someone else in the next game.

Finally

There's a lot of avenues (or rabbit holes?) we could go down for this. There's also plenty of third-party websites out there that facilitate FPL admin tasks. All things being equal, I found this to be a really fun application of OR Tools.

You can find the code for this post on my Github repo here.